Chu-Liu/Edmonds' Algorithm for Max Spanning Tree in Di-graph

In this blog, I will introduce the algorithm to find the maximum spanning tree in the directed graphs - the Chu-Liu/Edmonds’ Algorithm.

Problem Definition

Given a connected directed graph $G=\{V,E\}$ with vertices $V=\{v_1,v_2,...,v_n\}$ and edges $E=\{e_{12},...,e_{ij}\}$ , in which $e_{ij}$ represents the edge from vertex $v_i$ to $v_j$ with weight $w(e_{ij})$ the goal is to find the maximum spanning tree $T=\{V,E^t\}$ where all the vertices are connected, each node (except the root) has only one incoming edge, and the sum of weights of the edges is the maximum.

A Step-by-Step Explanation of Chu-Liu/Edmonds’ Algorithm

The Chu-Liu/Edmonds’ algorithm is designed in a recursive manner, to better explain the idea, I’ll show the algorithm step-by-step with an example.

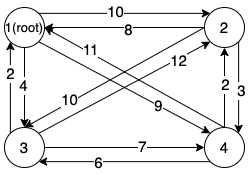
An example of a fully connected directed graph with four vertices.

Step Zero

Given the graph shown above, the first step is to decide the start point, i.e. the root of the tree. It can be predefined by the user, otherwise, the root is the node with the highest sum of outgoing edges, $r=\arg\max_{v_i\in V}\sum_{v_j \in V} e_{ji}$ . Then as the root can only have the outgoing edges, we remove all the incoming edges of the root.

In this case, the root is node 1 and after removing the unnecessary edges, the resulting graph is shown as:

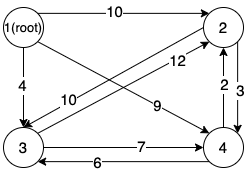
Step One

First, we start from the graph $MG$ with the maximum incoming edge for each node (other than the root), i.e. for each node $v_i$ , there is only one incoming edge from node $\pi(v_i)$ , denoting $e_{\pi(v_i)v_i}$ , and it is the edge with the maximum weight. If the graph is a tree, then it is the maximum spanning tree, otherwise, the graph contains at least one circle, then we need to break the circles by replacing certain edges with edges outside the graph $MG$ .

Back to the example, the green edges in the following graph forms the graph $MG$ , and we can find a circle between node $2$ and node $3$ .

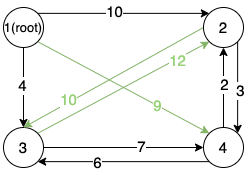
Step Two (recursive call)

Randomly picking one circle $C_{node}=\{v_{c_1},v_{c_2},...v_{c_k}\}$ in $MG$ , the circle itself is optimal, and we only need to break the circle with the minimum cost. To achieve this, we first build a new graph $G'$ by treating the circle as a new node $v_C$ , and then find the maximum spanning tree $A$ in the new graph $G'$ (recursively run the algorithm on $G'$ ).

Now we first decribe the way to build new graph $G'=\{V',E'\}$ with the vertex set $V'=V \setminus C\cup\{v_C\}$ . As for the edges $E'$ , we split them into three cases:

For edge $e_{sd}$ in $E$ , if $s\notin C_{node}$ and $d\in C_{node}$ , then we add an edge $e_{sv_C}'$ to $E'$ with weight $w(e_{sv_C}')=w(e_{sd})-w(e_{\pi(v_d)v_d})$ (it is a negative value)
For edge $e_{sd}$ in $E$ , if $s\in C_{node}$ and $d\notin C_{node}$ , then we add an edge $e_{v_Cd}'$ to $E'$ with weight $w(e_{v_C d}')=w(e_{sd})$
For edge $e_{sd}$ in $E$ , if $s\notin C_{node}$ and $d\notin C_{node}$ , then we add an edge $e_{sd}'$ to $E'$ with weight $w(e_{sd}')=w(e_{sd})$

Then there might be multiple edges between $v_C$ and other nodes, we only keep the edge with maximum weight between $v_C$ and each other node.

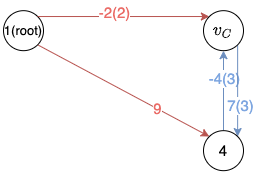
In this example, there is only one circle formed by node $2$ and node $3$ , so we treat the circle as a new node $v_C$ , as shown in the left figure below. Then by applying the rules mentioned above, we build the new graph $G'$ shown in the left. Apparently there are multiple edges between node $1,4$ and node $v_C$ , then we only keep the one with the highest weight (i.e. the blue edges, and the number in the parenthesis represents the original source/destinition of the edge in the circle).

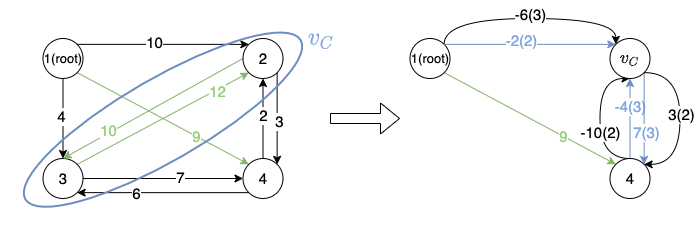
Then we need to find the maximum spanning tree $A$ for the new graph $G'$ , and it is formed by the edges in red in the figure below.

Step Three

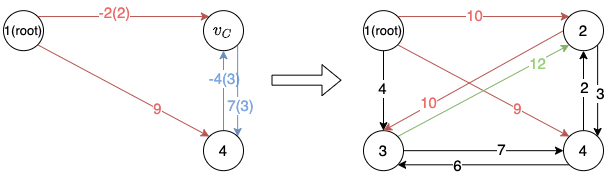
Without loss of generality, assume the incoming edge of $v_C$ in $A$ is from node $v_s$ and its corresponding edge in the original graph $G$ is $e_{sk}$ , with $v_k \in C_{node}$ , then the edges of the final tree is formed by the combination of edges in $A$ (replacing the edges from/to $v_C$ to the original edge) and the edges in the circle without the incoming edge of node $v_k$ .

As shown in the graph below, $E^t$ is formed by the red edges in the right figure.

We got it! Congrats! ^.^

Python Implementation

In this section, I’ll show my python implementation of the algorithm. There must be more efficient implementations, and discussions on improving the implementation are welcome.


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138

def reverse_graph(G):
    '''Return the reversed graph where g[dst][src]=G[src][dst]'''
    g={}
    for src in G.keys():
        for dst in G[src].keys():
            if dst not in g.keys():
                g[dst]={}
            g[dst][src]=G[src][dst]
    return g

def build_max(rg,root):
    '''Find the max in-edge for every node except for the root.'''
    mg = {}
    for dst in rg.keys():
        if dst==root:
            continue
        max_ind=-100
        max_value = -100
        for src in rg[dst].keys():
            if rg[dst][src]>=max_value:
                max_ind = src
                max_value = rg[dst][src]
        mg[dst]={max_ind:max_value}
    return mg

def find_circle(mg):
    '''Return the firse circle if find, otherwise return None'''
        
    for start in mg.keys():
        visited=[]
        stack = [start]
        while stack:
            n = stack.pop()
            if n in visited:
                C = []
                while n not in C:
                    C.append(n)
                    n = list(mg[n].keys())[0]
                return C
            visited.append(n)
            if n in mg.keys():
                stack.extend(list(mg[n].keys()))
    return None
        
def chu_liu_edmond(G,root):
    ''' G: dict of dict of weights
            G[i][j] = w means the edge from node i to node j has weight w.
            Assume the graph is connected and there is at least one spanning tree existing in G.
        root: the root node, has outgoing edges only.
    '''
    # reversed graph rg[dst][src] = G[src][dst]
    rg = reverse_graph(G)
    # root only has out edge
    rg[root]={}
    # the maximum edge for each node other than root
    mg = build_max(rg,root)
    
    # check if mg is a tree (contains a circle)
    C = find_circle(mg)
    # if there is no circle, it means mg is what we want
    if not C:
        return reverse_graph(mg)
    # Now consider the nodes in the circle C as one new node vc
    all_nodes = G.keys()
    vc = max(all_nodes)+1
    
    #The new graph G_prime with V_prime=V\C+{vc} 
    V_prime = list(set(all_nodes)-set(C))+[vc]
    G_prime = {}
    vc_in_idx={}
    vc_out_idx={}
    # Now add the edges to G_prime
    for u in all_nodes:
        for v in G[u].keys():
            # First case: if the source is not in the circle, and the dest is in the circle, i.e. in-edges for C
            # Then we only keep one edge from each node that is not in C to the new node vc with the largest difference (G[u][v]-list(mg[v].values())[0])
            # To specify, for each node u in V\C, there is an edge between u and vc if and only if there is an edge between u and any node v in C,
            # And the weight of edge u->vc = max_{v in C} (G[u][v] - mg[v].values) The second term represents the weight of max in-edge of v.
            # Then we record that the edge u->vc is originally the edge u->v with v=argmax_{v in C} (G[u][v] - mg[v].values)
            
            if (u not in C) and (v in C):
                if u not in G_prime.keys():
                    G_prime[u]={}
                w = G[u][v]-list(mg[v].values())[0]
                if (vc not in  G_prime[u]) or (vc in  G_prime[u] and w > G_prime[u][vc]):
                    G_prime[u][vc] = w
                    vc_in_idx[u] = v
            # Second case: if the source is in the circle, but the dest is not in the circle, i.e out-edge for C
            # Then we only keep one edge from the new node vc to each node that is not in C
            # To specify, for each node v in V\C, there is an edge between vc and v iff there is an edge between any edge u in C and v.
            # And the weight of edge vc->v = max_{u in C} G[u][v] 
            # Then we record that the edge vc->v originally the edge u->v with u=argmax_{u in C} G[u][v] 
            elif (u in C) and (v not in C):
                if vc not in G_prime.keys():
                    G_prime[vc]={}
                w = G[u][v]
                if (v not in  G_prime[vc]) or (v in  G_prime[vc] and w > G_prime[vc][v]):
                    G_prime[vc][v] = w
                    vc_out_idx[v] = u
            # Third case: if the source and dest are all not in the circle, then just add the edge to the new graph.
            elif (u not in C) and (v not in C):
                if u not in G_prime.keys():
                    G_prime[u]={}
                G_prime[u][v] = G[u][v]
    # Recursively run the algorihtm on the new graph G_prime
    # The result A should be a tree with nodes V\C+vc, then we just need to break the circle C and plug the subtree into A
    # To break the circle, we need to use the in-edge of vc, say u->vc to replace the original selected edge u->v, 
    # where v was the original edge we recorded in the first case above.
    # Then if vc has out-edges, we also need to replace them with the original edges, recorded in the second case above.
    A = chu_liu_edmond(G_prime,root)
    print(A)
    all_nodes_A = list(A.keys())
    for src in all_nodes_A:
        # The number of out-edges varies, could be 0 or any number <=|V\C|
        if src==vc:
            for node_in in A[src].keys():
                orig_out = vc_out_idx[node_in]
                if orig_out not in A.keys():
                    A[orig_out] = {}
                A[orig_out][node_in]=G[orig_out][node_in]
        else:
            for dst in A[src]:
                # There must be only one in-edge to vc.
                if dst==vc:
                    orig_in = vc_in_idx[src]
                    A[src][orig_in] = G[src][orig_in]
                    del A[src][dst]
    del A[vc]
    
    # Now add the edges from the circle to the result.
    # Remember not to include the one with new in-edge
    for node in C:
        if node != orig_in:
            src = list(mg[node].keys())[0]
            if src not in A.keys():
                A[src] = {}
            A[src][node] = mg[node][src]
    return A

Summary

In this blog, I introduced the traditional algorithm for finding the maximum/minimum spanning tree in the directed graph, and showed a python implementation of the algorithm. The algorithm is often used in the NLP area, especially in the topic like syntactic parsing/discourse parsing. Discussions on the implementation, the algorithm, or the applications are welcome.

Reference

[1] https://en.wikipedia.org/wiki/Edmonds%27_algorithm Wikipedia of Edmonds’ algorithm